Segment Trees (Part 1)

Introduction

The Segment Tree is a common data structure used to solve various range modification and query problems. For instance, consider the following problem:

• Given a known-length array of numbers with initial values, we need to perform multiple range addition operations (adding a value to all elements in a range) and range sum operations (calculating the sum of elements in a range).

Using a standard array, assuming the length og this array is N, each modification and query would take O(N) time. However, after constructing a Segment Tree in O(log N) time, both operations can be performed in O(log N), highlighting the importance of Segment Trees for range queries.

This example illustrates just one simple problem that Segment Trees can address. They can handle much more complex and interesting scenarios. In the upcoming articles, we will explore the concept of Segment Trees and how to implement them in MoonBit, ultimately creating a tree that supports range addition and multiplication, enables range sum queries, and has immutable properties.

In this section, we will learn the basic principles of Segment Trees and how to write a simple Segment Tree in MoonBit that supports point modifications and queries.

What is a Segment Tree?

This section focuses on concepts and theory. If you're already familiar with Segment Trees and their principles, feel free to skip to the next section.

As mentioned in the introduction, Segment Trees address a class of range problems, but what do they look like, and what is the principle behind their excellent complexity?

Let's consider a linear sequence of numbers as an example. If we want to build a Segment Tree from it, it will look like this:

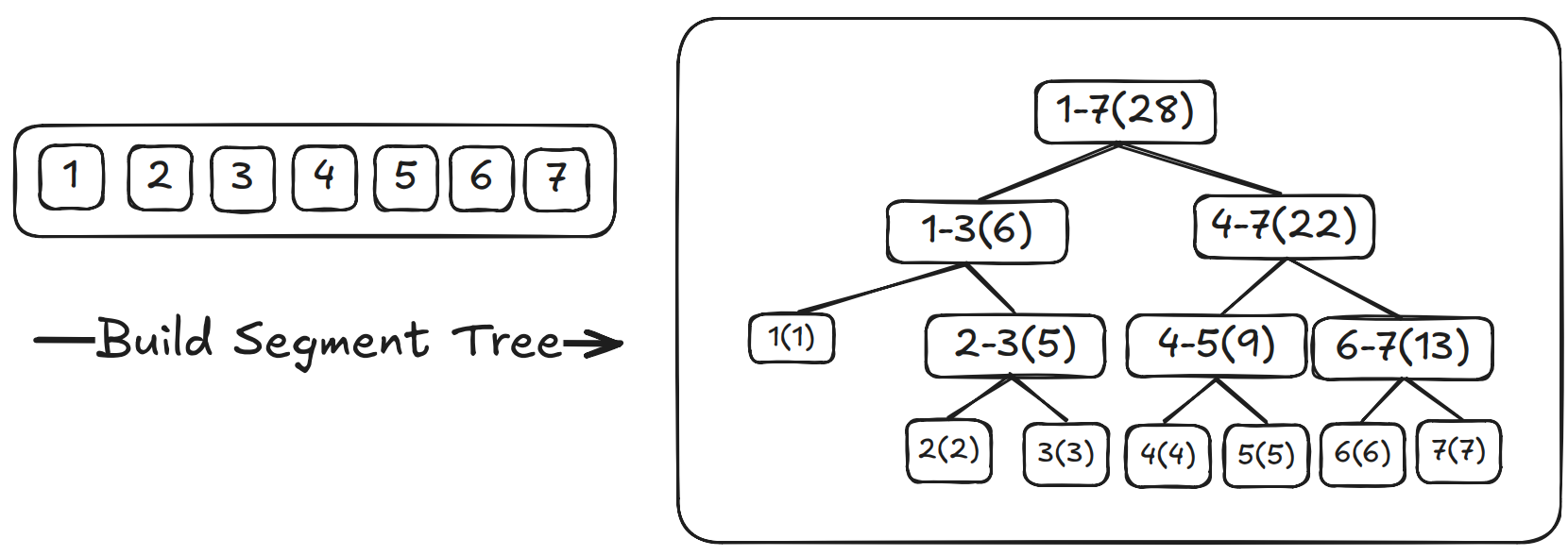
We can see that we recursively divide the linear sequence into two equal parts (with one side having an extra element if the length is odd) until we reach segments of length one. During this process, we compute the sum of each segment (shown in parentheses), thereby creating a Segment Tree that supports range sum queries from a linear sequence.

So, how does it work when querying a range sum? Let's take the example of querying the sum from index 1 to 6:

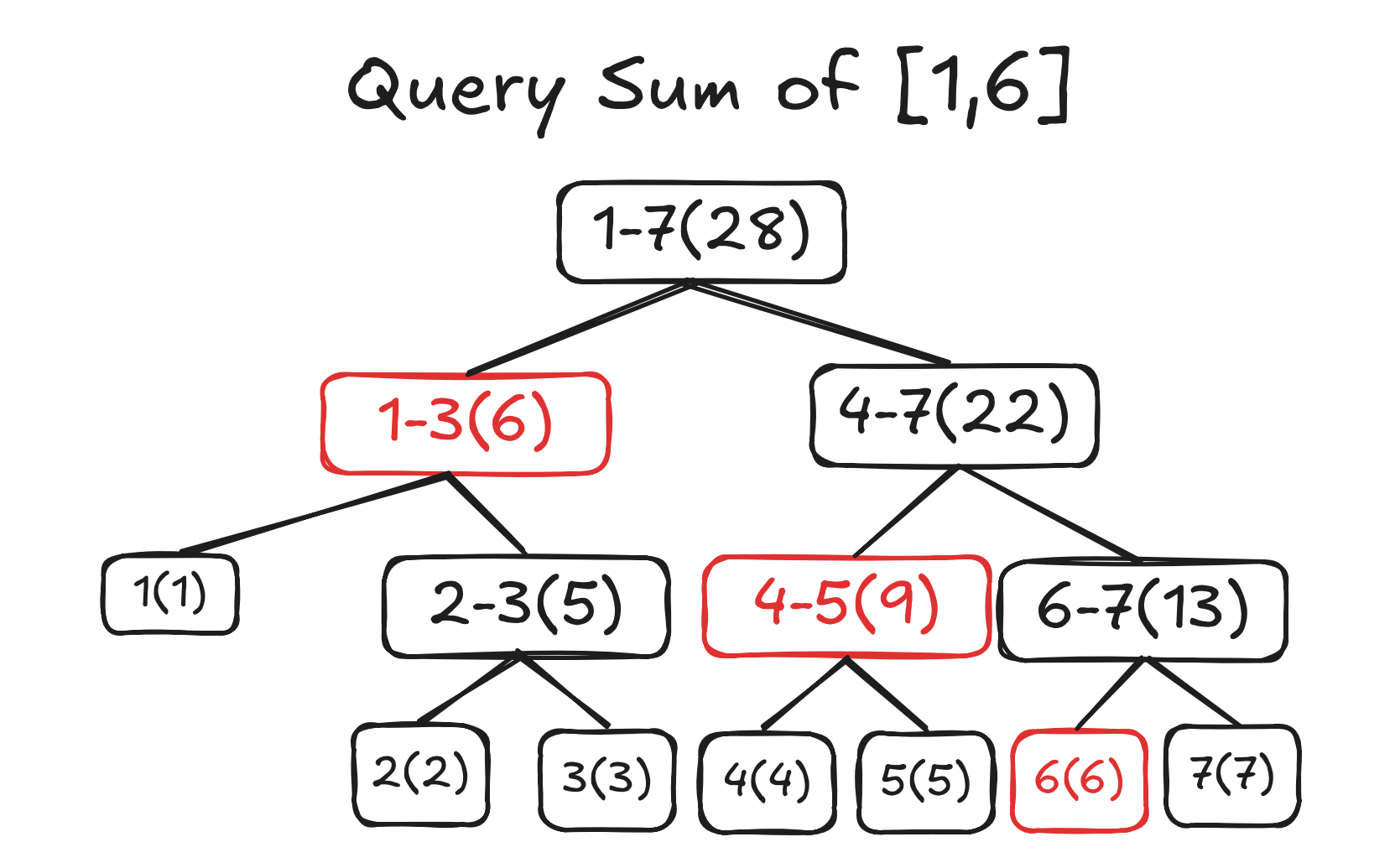
The highlighted parts in the diagram sum up to the total for the range 1-6, and we didn't have to consider all elements; we simply selected the minimum number of segments needed to obtain our result and combined them. We can traverse the Segment Tree from top to bottom to determine the intersections and containment relationships between segments to select the appropriate ranges.

Specifically:

• First, we check the relationship between the ranges 1-7 and 1-6. The latter is a subset of the former, so the data from 1-7 cannot be used in our calculation, and we proceed to explore its two child nodes.
• Next, we check the relationship between 1-3 and 1-6. The former is a subset of the latter, contributing to our result.
• Then, we examine the relationship between 4-7 and 1-6, which overlap, requiring us to explore both child nodes further.
• We repeat this process...

Based on binary decomposition, we will query at most Log N segments for any range of length N, ensuring guaranteed complexity.

This section only discusses the query operation; we will elaborate on the principles and implementation of modification operations in the next section.

Implementation

Basic Definition

We use a classic approach to represent the Segment Tree:

enum Node {
    Nil,
    Node(Int, Node, Node)
} derive(Show)

Here, Nil represents an empty tree, while a Node contains the stored data (of type Int) and its left and right children.

Additionally, we derive the Show Trait for easy debugging by outputting the tree structure when needed.

Building the Tree

Building the tree refers to the process of abstracting a linear sequence into a Segment Tree, commonly referred to as build.

To start, we should write an overloaded op_add function for the Node type to assist with the tree-building process:

fn op_add(self : Node, v : Node) -> Node {
    match (self, v) {
        (Node(left, _, _), Node(right, _, _)) => Node(left + right, self, v)
        (Node(_), Nil) => self
        (Nil, Node(_)) => v
        (Nil, Nil) => Nil
    }
}

With this operation defined, we can easily merge two Node instances while maintaining the segment sums, laying the foundation for building the tree. In some descriptions of Segment Trees, this process is also called pushup.

We can leverage MoonBit's ArrayView feature (known as slice in some languages) to recursively build the tree from a segment of a linear structure at a low cost, achieving O(Log N) complexity:

fn build(data : ArrayView[Int]) -> Node {
    if data.length() == 1 {
        Node(data[0], Nil, Nil)
    } else {
        let mid = (data.length() + 1) >> 1
        build(data[0:mid]) + build(data[mid:])
    }
}

Let’s analyze this code:

• If the current length is 1, the segment does not need further subdivision, so we return a leaf node with empty left and right branches.
• Otherwise, we split the segment at the midpoint and recursively build the left and right segments, then merge the results.

This code is concise, highly readable, and optimization-friendly, serving as a great learning paradigm for other data structures.

Now, let's build a tree and output it:

fn main {
    let tree = build([1, 2, 3, 4, 5][:])
    println(tree)
}

The output will be:

Node(15, Node(6, Node(3, Node(1, Nil, Nil), Node(2, Nil, Nil)), Node(3, Nil, Nil)), Node(9, Node(4, Nil, Nil), Node(5, Nil, Nil)))

Great! We've successfully built the tree!

Querying

Next, we need to implement the query function. Since the nodes of our Segment Tree maintain segment sums, we can write a query function to retrieve these sums:

let empty_node : Node = Node(0, Nil, Nil)

fn query(self : Node, l : Int, r : Int, query_l : Int, query_r : Int) -> Node {
    if query_l > r || l > query_r {
        empty_node
    } else if query_l <= l && query_r >= r {
        self
    } else {
        let Node(_, left, right) = self
        let mid = (l + r) >> 1
        left.query(l, mid, query_l, query_r) +
        right.query(mid + 1, r, query_l, query_r)
    }
}

Here, l and r represent the currently queried range, while query_l and query_r denote the range we need to query. Let's break down this implementation:

• If the queried range does not overlap with the current range, it contributes nothing to the result. We define an empty_node to represent a zero-contribution node and return it.
• If the current range is a subset of the queried range, it fully contributes to the result, so we return it directly.
• If the current range overlaps with the queried range, we continue searching downwards to find the exact covering ranges, merging the results of the left and right nodes.

Q&A

• Q: Why use Node as the return value? Can't I destructure and sum the values directly?

• A: We have defined an addition operation for Node. Consider a scenario where we need to maintain not just the sum but also the minimum value of a range. In that case, we can modify the op_add logic to maintain the minimum while the query function remains unaffected. It ultimately returns a Node that can contain all necessary information, so let's stick with using Node!

• Q: Shouldn't the empty_node change in this case?

• A: Yes, the empty_node ensures that it doesn’t affect the result when added to any other Node. It's a zero-contribution node, akin to how 0 contributes nothing in sum operations. For minimum value maintenance, it can represent a value that won't affect the outcome, making the process flexible!

Now, let's test the query process:

fn main {
    let tree = build([1, 2, 3, 4, 5][:])
    let sum = match tree.query(1, 5, 1, 3) {
        Node(sum, _, _) => sum
        _ => panic()
    }
    println(sum)
}

The output will be:

6

Fantastic! We've obtained the correct output!

Code

For the complete code, please check the GitHub repository.

Conclusion

Today, we learned how to build and query a simple Segment Tree. In the next lesson, we will explore more complex principles and implementations of Segment Trees. Interested readers can solidify their knowledge and expand on it by implementing the following:

• Try implementing a Segment Tree that maintains multiple pieces of information (e.g., range sum, maximum, and minimum).
• Understand how to implement point query/modification operations for Segment Trees.
• Explore range modification operations for Segment Trees and related Lazy Tags.